Перейти к:
Модель логистической регрессии для прогнозирования летальности в отделении интенсивной терапии: проблемы и решения
https://doi.org/10.37489/2588-0519-2022-2-13-20
Аннотация
Летальность в отделении интенсивной терапии является одной из важнейших метрик качества медицинской помощи. Цель исследования — создание модели прогноза летальности для пациентов с заболеваниями крови с использованием метода логистической регрессии и описание условий его применения при анализе данных. В исследование включили 202 пациента в возрасте от 19 до 82 лет (медиана — 57 лет), из них — 112 (55 %) мужчин и 90 (45 %) женщин. Статистический анализ проводился с использованием языка программирования R (версия 3.4.2). Вероятность смерти в отделении интенсивной терапии равнялась 33 % (67 из 202 пациентов), шансы — 0,496 (67/135). Согласно полученной модели снижение уровня тромбоцитов у пациента в 2 раза повышает шансы смерти в отделении интенсивной терапии на 31 %, или в 1,3 раза, снижение уровня общего белка в 2 раза — увеличивает шансы смерти в 11 раз, а любое нарушение сознания по шкале Глазго — почти в 20 раз при условии, что остальные переменные не изменяются. Чувствительность модели равнялась 82,3 %, специфичность — 80 %, точность — 81,6 % (95 % ДИ 67,9–91,2 %). Общая точность модели оказалась выше существующих шкал прогноза летальности qSOFA и MEWS, несмотря на простой метод анализа данных. Исследования в данной области необходимо продолжать.
Для цитирования:
Лучинин А.С., Лянгузов А.В. Модель логистической регрессии для прогнозирования летальности в отделении интенсивной терапии: проблемы и решения. Качественная клиническая практика. 2022;(2):13-20. https://doi.org/10.37489/2588-0519-2022-2-13-20
For citation:
Luchinin A.S., Lyanguzov A.V. A logistic regression-based model to predict ICU mortality: problems and solutions. Kachestvennaya Klinicheskaya Praktika = Good Clinical Practice. 2022;(2):13-20. (In Russ.) https://doi.org/10.37489/2588-0519-2022-2-13-20
Летальность — статистический показатель, необходимый для анализа деятельности каждого учреждения здравоохранения, но её прогноз — сложная техническая задача [1–3]. Летальность в отделении интенсивной терапии (ОИТ) является одной из важнейших метрик качества медицинской помощи. Возможность точного прогнозирования летальности пациентов в ОИТ позволит повысить эффективность планирования административно-организационных, санитарно-эпидемиологических и лечебно-диагностических мероприятий. Нами разработана собственная прогностическая модель для пациентов с заболеваниями крови, наблюдавшихся в ОИТ в период 2018–2021 гг. Для построения прогностической модели применён один из наиболее распространённых методов анализа данных — логистическая регрессия (ЛР), которая используется для описания взаимосвязей между переменными. Идея метода ЛР заключается в том, что условное пространство исходных значений зависимой переменной разделяется границей на две и более соответствующих классам области посредством математического метода максимального правдоподобия — данные разделяются с наибольшей вероятностью принадлежности исходного значения к определённому классу [4]. В нашем исследовании зависимой переменной являлась летальность в ОИТ, принимавшая два возможных категориальных значения: «да» или «нет». В случае прогнозирования двойного исхода ЛР называется биномиальной или бинарной.
В классическом виде уравнение ЛР представляет собой логит-функцию (натуральный логарифм отношения шансов (ОШ) изучаемого исхода):
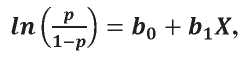
где p — вероятность прогнозируемого события;
b0 (интерсепт) — натуральный логарифм шансов исхода при условии нулевых значений всех независимых количественных переменных и/или начальной градации всех категориальных переменных;
b1 — коэффициент регрессии для предиктора X (натуральный логарифм отношения шансов для данной независимой переменной).
Число слагаемых коэффициентов регрессии равно числу независимых переменных.
Цель исследования / Aim
Создание модели прогнозирования летальности в ОИТ пациентов с онкогематологическими заболеваниями на основе ЛР.
Материалы и методы / Materials and methods
В исследование включили 202 пациента в возрасте от 19 до 82 лет (медиана — 57 лет), из них — 112 (55 %) мужчин и 90 (45 %) женщин. Показанием для госпитализации в ОИТ послужило тяжёлое состояние больных, связанное с инфекционными осложнениями, прогрессией заболевания или серьёзными побочными эффектами химиотерапии. Острый миелоидный лейкоз диагностировали у 82 пациентов, неходжкинские лимфомы и хронический лимфолейкоз — у 48, множественную миелому — у 24, острый лимфобластный лейкоз — у 18, лимфому Ходжкина — у 10, миелодиспластический синдром — у 12, хронические миелопролиферативные заболевания — у 6, апластическую анемию — у 1 и солидное злокачественное новообразование — у 1 больного.
Статистический анализ проводился с использованием языка программирования R (версия 4.1.2), библиотеки: missForest, glmnet, caret, MASS, DAAG, ResourceSelection, pROC.
Результаты / Results
1. Подготовка данных к анализу
Для создания модели ЛР следует проверить и выполнить ряд условий (допущений). Частично это проводилось на этапе подготовки данных к анализу, частично — в процессе и после построения модели. Все независимые переменные (предикторы, всего 21) разделили на два типа: количественные (возраст, температура тела, частота дыхания (ЧД), систолическое артериальное давление (АД), диастолическое АД, среднее АД, частота сердечных сокращений (ЧСС), количество баллов по шкале Глазго, уровень гемоглобина, число тромбоцитов и лейкоцитов в общем анализе крови, концентрация креатинина, С-реактивного белка (СРБ), общего белка, альбумина, общего билирубина и прокальцитонина в биохимическом анализе крови) и категориальные (пол, наличие инотропной поддержки катехоламинами, гипоксемия по данным парциального давления кислорода в крови или сатурации, бактериемия), их характеристика представлена в табл. 1. Значения предикторов получены в интервале ±2 дня от даты поступления в ОИТ.
Таблица 1
Характеристика предикторов
Table 1
Description of predictors

Примечание: 1 Количество пациентов (%) для категориальных переменных; медиана (минимум, максимум) для количественных переменных.
Note: 1 Number of patients (%) for categorical variables; median (minimum, maximum) for quantitative variables.
Все категориальные переменные являлись бинарными, то есть имели только 2 возможных значения. Несмотря на то что современные статистические программы могут работать с категориальными переменными с более чем двумя значениями, рекомендуется их трансформация в фиктивные (dummy) переменные. Фиктивные переменные представляют собой категории предикторов, записанные в бинарном виде (1/0), их число равно n-1, где n — количество исходных категорий [5][6]. Например, переменная пол, имеющая только два значения: «мужской» и «женский», — может быть трансформирована в фиктивную переменную «Пол мужской» со значениями 1 и 0, где 1 — мужчины, 0 — женщины. Перед проведением анализа все категориальные переменные в нашем исследовании были преобразованы подобным образом.
Другим методом трансформации данных является искусственное создание категориальной переменной из количественной и вместо неё. Такое преобразование не является обязательным и обычно выполняется для удобства последующей интерпретации созданной модели. Трансформация имеет эмпирический характер, то есть решение о способе преобразования принимает исследователь, основываясь на знаниях своей предметной области. В качестве вспомогательных могут быть использованы методы описательной статистики, например за межкатегориальный порог принимается медиана. В нашем исследовании категориальную трансформацию выполнили для шкалы комы Глазго, которая представлена в количественном виде в баллах от 3 до 15 (медиана 15). Новая бинарная переменная получила два значения: 1 и 0, где 0 — пациенты с уровнем сознания по шкале Глазго 15 баллов, 1 — менее 15 баллов.
Важным допущением к использованию ЛР, как и других методов многофакторного анализа, является размер выборки. Недостаточное количество наблюдений и событий понижает мощность статистического теста и увеличивает ошибки прогнозирования [7]. Эмпирический подход не даёт однозначного ответа о требуемом количестве событий (Events Per Predictor) — от 10 до 50 для каждого предиктора [8][9]. Существуют способы с использованием формул, например E=10*k/P и E=100+50k, где E — общее число событий, k — количество независимых переменных, P — частота изучаемого события [10][11]. В случае недостаточного числа событий следует сокращать количество предикторов, используя различные методы их выбора и/или снижения размерности, или отказаться от построения моделей прогноза [12][13]. При исходном числе независимых переменных в нашем исследовании (k=21) количество умерших для построения модели в зависимости от эмпирического подхода должно составлять от 210 до 1150. В связи с этим количество предикторов сократили разными способами, описанными ниже.
Исходная матрица данных из 202 наблюдений и 21 предиктора содержала 4242 значения, из них 103 (2,4 %) оказались пропущенными. Пропуск значений являлся следствием либо неназначения конкретного исследования, либо потери архивных данных. Наибольший дефицит информации наблюдался в отношении определения уровня прокальцитонина — 20,3 % пациентов. Также отсутствовали данные об уровне креатинина — у 3,5 % больных, С реактивного белка — у 5,4 %, общего белка — у 9,4 %, альбумина — у 8,9 %, общего билирубина — у 3,5 % пациентов. Проблему отсутствующих значений решили путём вменения на их место синтетических параметров, спрогнозированных с помощью модели машинного обучения — «случайный лес» (библиотека R missForest).
Важным фактором при построении прогностических моделей является сбалансированность данных по частоте изучаемого явления и предикторам. Очень низкая частота зависимой или независимых переменных приводит к асимметрии выборки, что в условиях малого числа наблюдений может нивелировать значимость тех или иных предикторов, приводить к различного рода парадоксам и в итоге понизить качество модели [14][15]. Частота положительного значения зависимой переменной — смертельного исхода — равнялась 33 %, что указывало на отсутствие проблемы несбалансированности данных. Проблема отсутствовала и в отношении независимых категориальных переменных (см. табл. 1).
На следующем этапе выполнили первую проверку на мультиколлинеарность — наличие корреляции независимых количественных переменных, которая может искажать коэффициенты регрессии модели [16]. Коллинеарными считались переменные, если коэффициенты корреляции Спирмена (ККС) равнялись более 0,75 по абсолютному значению. Корреляцию выявили между показателями систолического и диастолического АД (ККС=0,79), систолического и среднего АД (ККС=0,94), диастолического и среднего АД (ККС=0,95). В случае мультиколлинеарности необходимо выбрать один и удалить остальные коррелирующие предикторы из модели.
Несмотря на то что ЛР не требует нормального распределения количественных переменных, все их проверили на предмет выбросов — значений, находящихся за пределами полуторного межквартильного размаха от 1 и 3 квартилей. Наличие выбросов подтвердили у всех предикторов, кроме возраста, температуры тела и систолического АД. Избавление от выбросов является рекомендуемым, но не обязательным допущением ЛР [17][18]. Удаление выбросов путём исключения всего наблюдения из анализа является нерациональным, так как снижает общий размер выборки. В связи с этим применили метод логарифмирования всех количественных переменных по основанию 2. Выбор значения основания логарифма обусловлен более простой интерпретацией коэффициентов в модели регрессии. Следует отметить, что логарифм нулевого значения не может быть высчитан. У 1 из пациентов уровень тромбоцитов равнялся 0. Данное значение искусственно заменили на 1*109/л в рамках погрешности измерения гематологического анализатора, что не являлось критичным из-за отсутствия клинической значимости между уровнем тромбоцитов 0^109/л и 1^109/л.
2. Создание и тестирование модели
Вероятность смерти в ОИТ (абсолютный риск) равнялась 33 % (67 из 202 пациентов), шансы — 0,496 (67/135). Априорная вероятность клинического исхода может расцениваться как минимальная точность прогнозирования, известная до этапа моделирования. Целью прогнозного моделирования является создание более точной модели, чем известная априорная вероятность.
Перед началом моделирования выполнили случайное разделение (сплит) всей выборки на тренировочную (153 из 202, 75 % наблюдений) и тестовую (49 из 202, 25 % наблюдений). Модель создавали на тренировочной выборке, а проверяли на тестовой. Это является обязательным условием прогнозного моделирования, так как позволяет получить наиболее приближенную к реальным данным точность модели при проверке на данных, не принимавших участие в обучении [19].
Главной задачей при создании модели является правильный выбор предикторов, которые определяют её конечную прогнозную эффективность. Выбор предикторов — это не единовременный, а, как правило, динамический процесс на протяжении всего научного эксперимента. Начальный набор предикторов может меняться в зависимости от получаемого качества модели. Обучение повторяется до тех пор, пока точность прогноза не становится максимальной. Селекция предикторов состоит из двух этапов. Первый — включает в себя формирование стартового списка независимых переменных, базовыми принципами которого могут быть эмпирический подход, основанный на субъективном мнении исследователя, метод Хосмера — Лемешоу — выбор предикторов по результатам однофакторного анализа [20] — и методы регуляризации. На втором этапе количество предикторов при необходимости искусственно снижается вручную или автоматическими методами последовательного отбора, например пошаговой регрессией (stepwise) [21]. В нашем исследовании эмпирический подход указывал на нерациональность использования в модели высоко коррелирующих между собой предикторов из-за проблемы мультиколлинеарности: систолическое, диастолическое и среднее АД. В однофакторном анализе все три предиктора, связанные с АД, показали свою статистическую значимость с отрицательными коэффициентами регрессии (снижение АД увеличивает шансы умереть). Следует отметить, что в качестве порога статистической значимости альфа при таком подходе рекомендуется использовать значение 0,25 вместо 0,05. Это обосновано снижением риска ложного исключения потенциально важных предикторов. Тем не менее, даже при таком подходе, метод Хосмера — Лемешоу нельзя считать идеальным [20]. После того, как все предикторы включили в многофакторный анализ, коэффициент регрессии для среднего АД стал положительным, при сохранении отрицательных коэффициентов для систолического и диастолического АД, что следует интерпретировать как снижение риска смерти при снижении среднего АД и наоборот. Кроме того, предикторы утратили статистическую значимость, превзойдя порог альфа, равный 0,25. Это явление наиболее известно в статистике как парадокс Симпсона, когда при объединении нескольких групп данных, в каждой из которых по отдельности наблюдается одинаково направленная зависимость, её направление меняется на противоположное. Одной из причин парадокса Симпсона, наряду с несбалансированными данными, является мультиколлинеарность [15].
Для снижения количества предикторов, что являлось необходимым шагом из-за ограниченного размера выборки и известных недостатков метода Хосмера — Лемешоу, использовали регрессию «лассо» (LASSO, Least Absolute Shrinkage and Selection Operator) (библиотеки R caret, glmnet). Этот подход решает сразу две задачи: автоматический выбор наилучших предикторов и регуляризацию — стратегия, направленная на снижение ошибки обобщения (переобучения модели) [22][23]. Регуляризация помогает создать более простые модели, которые, как утверждает методологический принцип бритвы Оккама, скорее всего, будут работать лучше. Оптимальную величину параметра регуляризации лямбда, при которой ошибка прогноза минимальна, нашли в результате 10-кратной кросс-валидации на тренировочном наборе данных. По результатам регрессии «лассо» выбрали предикторы: ЧСС, гипоксемия, уровень тромбоцитов, уровни общего белка, альбумина и общего билирубина в крови, уровень сознания по шкале Глазго в виде бинарной переменной, где 1 — количество баллов менее 15 и 0 — равно 15. Следующим шагом было обучение модели ЛР с выбранными переменными. Количественные параметры прологарифмировали по основанию 2. В качестве показателя точности модели использовали информационный критерий Акаике (AIC). Данный критерий применяется для выбора лучшей из нескольких статистических моделей, построенных на одном и том же наборе данных и использующих логарифмическую функцию правдоподобия, чем его значение меньше, тем модель лучше [24]. Последовательный отбор моделей осуществляли методом пошаговой регрессии (stepwise), при котором фактор является незначимым, если его включение или исключение из уравнения регрессии значительно не меняет суммы квадратов остатков (ошибок прогноза) [21].
Итоговая модель ЛР выглядела следующим образом:

Характеристика модели представлена в табл. 2.
Таблица 2
Характеристика итоговой модели ЛР
Table 2
Description of logistic regression model

Примечание: ОШ — отношение шансов; 95 % ДИ — 95 % доверительный интервал.
Notes: OR — odds ratio; 95 % CI — 95 % confi dence interval.
Таким образом, снижение уровня тромбоцитов у пациента в 2 раза повышает шансы смерти в ОИТ на 31 %, или в 1,3 раза, снижение уровня общего белка в 2 раза — увеличивает шансы смерти в 11 раз, а любое нарушение сознания по шкале Глазго — почти в 20 раз при условии, что остальные переменные не изменяются.
После построения модели выполнили ряд дополнительных проверок её качества. Вначале сделали повторный тест на мультиколлинеарность c помощью оценки фактора инфляции вариации (VIF), который оценивает влияние одной независимой переменной на все остальные независимые переменные (библиотека R DAAG). Значение VIF для всех предикторов равнялось менее 5, что расценивалось как отсутствие коллинеарности между ними [25].
Одним из важнейших предположений ЛР является линейность взаимосвязи между логитом (логарифмом ОШ) результата модели и каждой независимой количественной переменной. Для проверки используется тест Бокса — Тидвелла путём анализа взаимодействия между непрерывными независимыми переменными и их соответствующим натуральным логарифмом [26]. Обе количественные переменные (уровни тромбоцитов и общего белка в крови) прошли проверку на предположение линейной взаимосвязи с логитом результата.
В заключение, прежде чем полагаться на модель и предсказывать будущие результаты, нами выполнен тест соответствия Хосмера — Лемешоу (библиотека R ResourceSelection). Тест оценивает, соответствует ли (не имеет ли статистически значимых отличий) прогнозируемая вероятность событий во всей выборке таковой в отдельных её подгруппах [27]. Признаков несоответствия модели и данных не обнаружили (χ2=0,45; p=0,48).
Согласно модели, для всех клинических случаев тренировочного набора данных высчитали вероятность летального исхода в ОИТ, которая колебалась в пределах от 0,9 % до 96,4 % (медиана — 25,6 %). Для выявления прогностического порога вероятности смерти применили ROC-анализ (библиотеки R pROC и OptimalCutpoints), в качестве классифицирующей варианты использовали статус пациента при завершении лечения пациента в ОИТ (умер жив). Оптимальное значение порога активации (так называемого cut-off ), вычисленное по методике Юдена (максимальное расстояние от диагональной линии до ROC-кривой) [28], равнялось 32,1 %. При этом значении модель имеет максимальную точность, что определяется площадью под ROC-кривой (AUC = 0,77) (рис. 1).
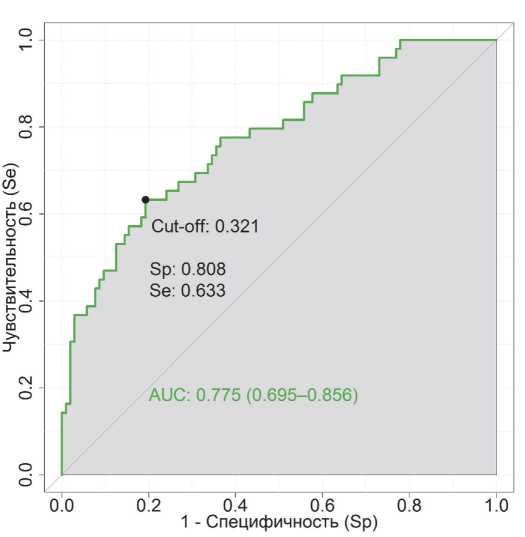
Рис. 1. Модель прогноза летальности в ОИТ
Fig. 1. ICU mortality prediction model
Проверка прогностической точности модели проводилась на тестовой выборке (49 пациентов), данные которой не использовались в обучении. Согласно модели, для всех клинических случаев высчитали вероятность летального исхода в ОИТ. Пациентов классифицировали на группы с положительным (вероятность >32 %) и отрицательным (вероятность ≤32 %) прогнозом смерти в ОИТ и сравнили с их известным исходом. Чувствительность модели равнялась 82,3 %, специфичность — 80 %, точность — 81,6 % (95 % ДИ 67,9–91,2 %), p-уровень значимости теста Макнемара = 0,504 (истинная и предсказанная пропорции умерших статистически значимо не отличаются друг от друга).
Созданную модель прогноза сравнили с существующими балльными шкалами оценки риска летальности в ОИТ qSOFA [29] и MEWS [30] (табл. 3). Точность новой модели и её характеристики оказались лучше, однако для дальнейшей проверки требуется увеличение объёма валидирующей выборки с включением пациентов из других медицинских центров.
Таблица 3
Сравнение моделей прогноза летальности
Table 3
Comparison of mortality prediction models

Обсуждение / Discussion
Прогнозная аналитика — сложная область медицины ввиду специфики задач, которые приходится решать, и требований к их исполнению. Прогноз летальности зависит от большого числа самых разных факторов, некоторые из которых не всегда можно учесть. Наше исследование является одним из примеров решения данной проблемы в условиях реальной клинической практики. Мы применили один из самых доступных методов анализа данных — ЛР. Как и более сложные методы машинного обучения, ЛР не является универсальным способом прогнозирования. Использование ЛР требует соблюдения ряда важных допущений или условий, которые подробно описаны. Их игнорирование может стать причиной низкого качества прогностической модели или привести к неверным результатам. Самым главным условием при создании любой модели прогноза, независимо от статистического метода, является раздельное обучение на тренировочном наборе данных с последующей проверкой результатов на тестовой выборке, что исключает проблемы переобучения и подгонки результатов [19].
В процессе создания модели прогноза исследователь может решать две основные задачи. Первая — поиск предикторов — факторов, значимо влияющих на изучаемый исход. Если данная задача является конечной целью научного исследования, эксперимент прекращается до этапа тестирования модели. В нашем исследовании наиболее значимыми, но не единственными независимыми факторами прогноза являлись количество тромбоцитов и общего белка в крови, а также уровень сознания по шкале Глазго, представленный в виде бинарной переменной. Эти клинические параметры являются наиболее значимыми у гематологических больных и требуют мониторинга и максимального внимания со стороны врача. Их сочетанная оценка лежит в основе достаточно простой и точной модели прогнозирования летальности в условиях ОИТ, которую мы смогли получить. Второй задачей прогнозной аналитики является собственно создание прогностической модели с целью предсказания исходов заболеваний. Точность описанной модели на тестовой выборке составила 81,6 % при чувствительности 82,3 % и специфичности 80 %.
Чувствительность модели — доля истинно положительных результатов, при которой модель правильно предсказывает наличие прогнозируемого события (чувствительность может быть от 0 до 100 %). Специфичность — доля истинно отрицательных результатов, когда модель правильно предсказывает отсутствие прогнозируемого события (специфичность может быть от 0 до 100 %) [31]. Эти параметры лежат в основе оценки качества моделей машинного обучения и искусственного интеллекта (ИИ) в медицине. Современными требованиями к медицинским системам ИИ в России для их применения в клинической практике, по мнению ряда экспертов, являются показатели чувствительности от 95 % и выше и специфичности — от 80 % и выше, подтверждённые при валидации в рамках клинических исследований. Созданная модель не позволила достичь указанных параметров по ряду объективных причин, в частности из-за ограниченных возможностей ЛР как метода анализа данных, который считается достаточно простым. Тем не менее общая точность модели оказалась выше традиционных шкал qSOFA и MEWS (81,6 %), что свидетельствует о перспективности дальнейших исследований в данной области.
В заключение следует отметить, что популярность использования цифровых решений в медицине в настоящее время ведёт к росту риска технических и логических ошибок исследователей в погоне за трендом. Научные исследования, по результатам которых формируются практические рекомендации, требуют не только знаний предметной области, но и хорошей теоретической подготовки в анализе данных и статистике. Так как за любой научной гипотезой в медицине стоит здоровье или жизнь пациента, цена ошибки крайне высока, а любые спекуляции — неприемлемы.
ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
ADDITIONAL INFORMATION
Конфликт интересов отсутствует.
Conflict of interests. Absence of Conflict of Interest.
Список литературы
1. Lee J, Dubin JA, Maslove DM. Mortality Prediction in the ICU // Secondary Analysis of Electronic Health Records / ed. MIT Critical Data. Cham: Springer International Publishing, 2016. P. 315–324.
2. Pirracchio R, Petersen ML, Carone M, et al. Mortality prediction in the ICU: can we do better? Results from the Super ICU Learner Algorithm (SICULA) project, a population-based study. Lancet Respir Med. 2015;3(1):42– 52. doi: 10.1016/S2213-2600(14)70239-5
3. Awad A, Bader-El-Den M, McNicholas J, et al. Predicting hospital mortality for intensive care unit patients: Time-series analysis. Health Informatics J. SAGE Publications Ltd, 2020;26(2):1043–59. doi: 10.1177/1460458219850323
4. Schober P, Vetter TR. Logistic Regression in Medical Research. Anesth Analg. 2021;132(2):365–6. doi: 10.1213/ANE.0000000000005247
5. Ahmed SN, Jhaj R, Sadasivam B, et al. Reversal of hypertensive heart disease: a multiple linear regression model. Discoveries (Craiova). 2021;9(4):e138.
6. Lunt M. Introduction to statistical modelling 2: categorical variables and interactions in linear regression. Rheumatology (Oxford). 2015;54(7):1141–4. doi: 10.1093/rheumatology/ket172
7. Serdar CC, Cihan M, Yücel D, et al. Sample size, power and effect size revisited: simplified and practical approaches in pre-clinical, clinical and laboratory studies. Biochem Med (Zagreb). 2021;31(1):010502. doi: 10.11613/BM.2021.010502
8. Jenkins DG, Quintana-Ascencio PF. A solution to minimum sample size for regressions. PLoS One. 2020;15(2):e0229345. doi: 10.1371/journal.pone.0229345
9. Wilson Van Voorhis CR, Morgan BL. Understanding Power and Rules of Thumb for Determining Sample Size. TQMP. 2007;3(2):43–50. doi: 10.20982/tqmp.03.2.p043
10. Peduzzi P, Concato J, Kemper E, et al. A simulation study of the number of events per variable in logistic regression analysis. J Clin Epidemiol. 1996;49(12):1373–9. doi: 10.1016/s0895-4356(96)00236-3
11. Bujang MA, Sa’at N, Sidik TMITAB, Joo LC. Sample Size Guidelines for Logistic Regression from Observational Studies with Large Population: Emphasis on the Accuracy Between Statistics and Parameters Based on Real Life Clinical Data. Malays J Med Sci. 2018;25(4):122–30. doi: 10.21315/mjms2018.25.4.12
12. Ajana S, Acar N, Bretillon L, et al. Benefits of dimension reduction in penalized regression methods for high-dimensional grouped data: a case study in low sample size. Bioinformatics. 2019;35(19):3628–34. doi: 10.1093/bioinformatics/btz135
13. Santana AC, Barbosa AV, Yehia HC, et al. A dimension reduction technique applied to regression on high dimension, low sample size neurophysiological data sets. BMC Neurosci. 2021;22(1):1. doi: 10.1186/s12868-020-00605-0
14. Ishwaran H, O’Brien R. Commentary: The problem of class imbalance in biomedical data. J Thorac Cardiovasc Surg. 2021;161(6):1940–1. doi: 10.1016/j.jtcvs.2020.06.052
15. Ameringer S, Serlin RC, Ward S. Simpson’s Paradox and Experimental Research. Nurs Res. 2009;58(2):123–7. doi: 10.1097/NNR.0b013e318199b517
16. Senaviratna NaMR, Cooray TMJA. Diagnosing Multicollinearity of Logistic Regression Model. Asian Journal of Probability and Statistics. 2019;1– 9. doi: 10.9734/ajpas/2019/v5i230132
17. Cutanda Henríquez F. [Outliers and robust logistic regression in Health Sciences]. Rev Esp Salud Publica. 2008;82(6):617–25. doi: 10.1590/s1135-57272008000600003
18. Zhang Y, Zhou X, Wang Q, et al. Quality of reporting of multivariable logistic regression models in Chinese clinical medical journals. Medicine (Baltimore). 2017;96(21):e6972. doi: 10.1097/MD.0000000000006972
19. Altman DG, Vergouwe Y, Royston P, et al. Prognosis and prognostic research: validating a prognostic model. BMJ. 2009;338:b605. doi: 10.1136/bmj.b605
20. Sun GW, Shook TL, Kay GL. Inappropriate use of bivariable analysis to screen risk factors for use in multivariable analysis. J Clin Epidemiol. 1996;49(8):907–16. doi: 10.1016/0895-4356(96)00025-x
21. Zhang Z. Variable selection with stepwise and best subset approaches. Ann Transl Med. 2016;4(7):136. doi: 10.21037/atm.2016.03.35
22. Tibshirani R. The lasso method for variable selection in the Cox model. Stat Med. 1997;16(4):385–95. doi: 10.1002/(sici)1097-0258(19970228)16:4>385::aid-sim380<3.0.co;2-3
23. Musoro JZ, Zwinderman AH, Puhan MA, et al. Validation of prediction models based on lasso regression with multiply imputed data. BMC Med Res Methodol. 2014;14:116. doi: 10.1186/1471-2288-14-116
24. Dziak JJ, Coffman DL, Lanza ST, et al. Sensitivity and specificity of information criteria. Brief Bioinform. 2020;21(2):553–65. doi: 10.1093/bib/bbz016
25. Kim JH. Multicollinearity and misleading statistical results. Korean J Anesthesiol. 2019;72(6):558–69. doi: 10.4097/kja.19087
26. Li B, Martin EB, Morris AJ. Box–Tidwell transformation based partial least squares regression. Computers & Chemical Engineering. 2001;25(9):1219–33.
27. Nattino G, Pennell ML, Lemeshow S. Assessing the goodness of fit of logistic regression models in large samples: A modification of the Hosmer-Lemeshow test. Biometrics. 2020;76(2):549–60. doi: 10.1111/biom.13249
28. Fluss R, Faraggi D, Reiser B. Estimation of the Youden Index and its associated cutoff point. Biom J. 2005;47(4):458–72. doi: 10.1002/bimj.200410135
29. Abdullah SMOB, Grand J, Sijapati A, et al. qSOFA is a useful prognostic factor for 30-day mortality in infected patients fulfilling the SIRS criteria for sepsis. Am J Emerg Med. 2020;38(3):512–6. doi: 10.1016/j.ajem.2019.05.037
30. Roney JK, Whitley BE, Maples JC, et al. Modified early warning scoring (MEWS): evaluating the evidence for tool inclusion of sepsis screening criteria and impact on mortality and failure to rescue. J Clin Nurs. 2015;24(23–24):3343– 54. doi: 10.1111/jocn.12952
31. Лучинин А. С. Искусственный интеллект в гематологии. Клиническая онкогематология. 2022;15(1):16–27. doi: 10.21320/2500-2139-2022-15-1-16-27
Об авторах
А. С. ЛучининРоссия
Лучинин Александр Сергеевич - кандидат медицинских наук, старший научный сотрудник отдела организации и сопровождения научных исследований КНИИГиПК ФМБА России.
Киров.
А. В. Лянгузов
Россия
Лянгузов Алексей В. - кандидат медицинских наук, КНИИГиПК ФМБА России.
Киров.
Рецензия
Для цитирования:
Лучинин А.С., Лянгузов А.В. Модель логистической регрессии для прогнозирования летальности в отделении интенсивной терапии: проблемы и решения. Качественная клиническая практика. 2022;(2):13-20. https://doi.org/10.37489/2588-0519-2022-2-13-20
For citation:
Luchinin A.S., Lyanguzov A.V. A logistic regression-based model to predict ICU mortality: problems and solutions. Kachestvennaya Klinicheskaya Praktika = Good Clinical Practice. 2022;(2):13-20. (In Russ.) https://doi.org/10.37489/2588-0519-2022-2-13-20
















































